Common Cryptographic Algorithms

There are two basic kinds of encryption algorithms in use today:

Private key cryptography is most often used for protecting information stored on a computer's hard disk, or for encrypting information carried by a communications link between two different machines. Public key cryptography is most often used for creating digital signatures on data, such as electronic mail, to certify the data's origin and integrity.

This analysis gives rise to a third kind of system:

Summary of Private Key Systems

The following list summarizes the private key systems in common use today.

Summary of Public Key Systems

The following list summarizes the public key systems in common use today:

Table 6.1 lists all of the private and public key algorithms we've discussed

Commonly Used Private and Public Key Cryptography Algorithms
Algorithm Description

Private Key Algorithms:

ROT13 Keyless text scrambler; very weak.
crypt Variable key length stream cipher; very weak.[12]
DES -bit block cipher; patented, but freely usable (but not exportable).
RC2 Variable key length block cipher; proprietary.
RC4 Variable key length stream cipher; proprietary.
RC5 Variable key length block cipher; proprietary.
IDEA -bit block cipher; patented.
Skipjack -bit stream cipher; classified.

Public Key Algorithms:

Diffie-Hellman Key exchange protocol; patented.
RSA Public key encryption and digital signatures; patented
ElGamal Public key encryption and digital signatures; patented.
DSA Digital signatures only; patented.

[12] Actually, crypt is a fair cipher for files of length less than 1024 bytes. Its recurrence properties only surface when used on longer inputs, thus providing more information for decrypting.

The following sections provide some technical information about a few of the algorithms mentioned above. If you are only interested in using encryption, you can skip ahead to the section called "Encryption Programs Available for UNIX" later in this chapter.

ROT13: Great for Encoding Offensive Jokes

ROT13 is a simple substitution cipher[13] that is traditionally used for distributing potentially objectionable material on the Usenet, a worldwide bulletin board system. It is a variation on the Caesar Cipher - an encryption method used by Caesar's troops thousands of years ago. In the ROT13 cipher, each letter of the alphabet is replaced with a letter that is 13 letters further along in the alphabet (with A following Z). Letters encrypt as follows:

[13] Technically, it is an encoding scheme - the "rotation" is fixed, and it does a constant encoding from a fixed alphabet.

Plaintext Ciphertext
A N
B O
M Z
N A
Z M

ROT13 used to be the most widely used encryption system in the UNIX world. However, it is not secure at all. Many news and mail-reading programs automatically decrypt ROT13-encoded text with a single keystroke. Some people are known to be able to read ROT13 text without any machine assistance whatsoever.

For example, here is a ROT13 message: 

Jung tbrf nebhaq, pbzrf nebhaq.

And here is how the message decrypts: 

What goes around, comes around.

If you are not blessed with the ability to read ROT13 files without computer assistance, you can use the following command to either encrypt or decrypt files with the ROT13 algorithm:[14]

[14] On some versions of UNIX, you will need to remove the "[ ]" symbols.



% tr "[a-z][A-Z]" "[n-z][a-m][N-Z][A-M]" < filename

Needless to say, do not use ROT13 as a means of protecting your files! The only real use for this "encryption" method is the one to which it is put on the Usenet: to keep someone who does not want to be exposed to material (such as the answer to a riddle, a movie spoiler in a review, or an offensive joke) from reading it inadvertently.

DES

One of the most widely used encryption systems today is the Data Encryption Standard (DES), developed in the 1970s and patented by researchers at IBM. The DES was an outgrowth of another IBM cipher known as Lucifer. IBM made the DES available for public use, and the federal government issued Federal Information Processing Standard Publication (FIPS PUB) Number 46 in 1977 describing the system. Since that time, the DES has been periodically reviewed and reaffirmed (most recently in December 30, 1993), until 1998 as FIPS PUB 46-2. It has also been adopted as an American National Standard (X3.92-1981/R1987).

The DES performs a series of bit permutation, substitution, and recombination operations on blocks containing 64 bits of data and 56 bits of key (eight 7-bit characters). The 64 bits of input are permuted initially, and are then input to a function using static tables of permutations and substitutions (called S-boxes). The bits are permuted in combination with 48 bits of the key in each round. This process is iterated 16 times (rounds), each time with a different set of tables and different bits from the key. The algorithm then performs a final permutation, and 64 bits of output are provided. The algorithm is structured in such a way that changing any bit in the input has a major effect on almost all of the output bits. Indeed, the output of the DES function appears so unrelated to its input that the function is sometimes used as a random number generator.

Although there is no standard UNIX program that performs encryption using the DES, some vendors' versions of UNIX include a program called des which performs DES encryption. (This command may not be present in international versions of the operating system, as described in the next section.)

Use and export of DES

The DES was mandated as the encryption method to be used by all federal agencies in protecting sensitive but not classified information.[15] The DES is heavily used in many financial and communication exchanges. Many vendors make DES chips that can encode or decode information fast enough to be used in data-encrypting modems or network interfaces. Note that the DES is not (and has never been) certified as an encryption method that can be used with U.S. Department of Defense classified material.

[15] Other algorithms developed by the NSA are designed for use with classified information.

Export control rules restrict the export of hardware or software implementations of the DES, even though the algorithm has been widely published and implemented many times outside the United States. If you have the international version of UNIX, you may find that your system lacks a des command. If you find yourself in this position, don't worry; good implementations of the DES can be obtained via anonymous FTP from almost any archive service, including the Usenet comp.sources archives.

For more information about export of cryptography, see "Encryption and jungle law," later in this chapter.

DES modes

FIPS PUB 81 explains how the DES algorithm can be used in four modes:

Each mode has particular advantages in some circumstances, such as when transmitting text over a noisy channel, or when it is necessary to decrypt only a portion of a file. The following provides a brief discussion of these four methods; consult FIPS PUB 81 or a good texttutorial on cryptography for details.

All of these modes require that byte and block boundaries remain synchronized between the sender and recipient. If information is inserted or removed from the encrypted data stream, it is likely that all of the following data from the point of modification can be rendered unintelligible.

DES strength

Ever since DES was first proposed as a national standard, some people have been suspicious of the algorithm. DES was based on a proprietary encryption algorithm developed by IBM called Lucifer, which IBM had submitted to the National Bureau of Standards (NBS)[16] for consideration as a national cryptographic standard. But whereas Lucifer had a key that was 112 bits long, the DES key was shortened to 56 bits at the request of the National Security Agency. The NSA also requested that certain changes be made in the algorithm's S-boxes. Many people suspected that NSA had intentionally weakened the Lucifer algorithm, so the final standard adopted by NBS would not pose a threat to the NSA's ongoing intelligence collection activities. But nobody had any proof.

[16] NBS later became the National Institute of Standards and Technology.

Today the DES is more than 20 years old, and the algorithm is definitely showing its age. Recently Michael Weiner, a researcher at Bell Northern Research, published a paper detailing how to build a machine capable of decrypting messages encrypted with the DES by conducting an exhaustive key search. Such a machine could be built for a few million dollars, and could break any DES-encrypted message in about a day. We can reasonably assume that such machines have been built by both governments and private industry.

In June 1994, IBM published a paper describing the design criteria of the DES. The paper claims that the choices of the DES key size, S-boxes, and number of rounds were a direct result of the conflicting goals of making the DES simple enough to fit onto a single chip with 1972 chip-making technology, and the desire to make it resistant to differential cryptanalysis.

These two papers, coupled with many previously published analyses, appear to have finally settled a long-running controversy as to whether or not NSA had intentionally built in weaknesses to the DES. The NSA didn't build a back door into DES that would have allowed it to forcibly decrypt any DES-encrypted transmission: it didn't need to. Messages encrypted with DES can be forcibly decrypted simply by trying every possible key, given the appropriate hardware.

Improving the Security of DES

You can improve the security of DES by performing multiple encryptions, known as superencryption. The two most common ways of doing this are with double encryption (Double DES) and with triple encryption (Triple DES).

While double DES appears to add significant security, research has found some points of attack, and therefore experts recommend Triple DES for applications where single DES is not adequate.

Double DES

In Double DES, each 64-bit block of data is encrypted twice with the DES algorithm, first with one key, then with another, as follows:

  1. Encrypt with (key 1).
  2. Encrypt with (key 2).

Plaintext 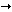->(key1) 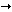->(key2) 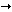->ciphertext

Double DES is not significantly more secure than single DES. In 1981, Ralph Merkle and Martin Hellman published an article[17] in which they outlined a so-called "meet-in-the-middle attack."

[17] R. C. Merkle and M. Hellman, "On the Security of Multiple Encryption," Communications of the ACM, Volume 24, Number 7, July 1981, pp. 465-467.

The meet-in-the-middle attack is a known plaintext attack which requires that an attacker have both a known piece of plaintext and a block of that same text that has been encrypted. (These pieces are surprisingly easily to get.) The attack requires storing 2 intermediate results when trying to crack a message that has been encrypted with DES (a total of 2 bytes), but it reduces the number of different keys you need to check from 2 to 2. "This is still considerably more memory storage than one could comfortably comprehend, but it's enough to convince the most paranoid of cryptographers that double encryption is not worth anything," writes Bruce Schneier in his landmark volume, Applied Cryptography.

In other words, because a message encrypted with DES can be forcibly decrypted by an attacker performing an exhaustive key search today, an attacker might also be able to forcibly decrypt a message encrypted with Double DES using a meet-in-the-middle attack at some point in the future.

Triple DES

The dangers of the Merkle-Hellman meet-in-the-middle attack can be circumvented by performing three block encryption operations. This method is called Triple DES.

In practice, the most common way to perform Triple DES is:

  1. Encrypt with (key1).
  2. Decrypt with (key2).
  3. Encrypt with (key3).

The advantage of this technique is that it can be backward compatible with single DES, simply by setting all three keys to be the same value.

To decrypt, reverse the steps:

  1. Decrypt with (key3).
  2. Encrypt with (key2).
  3. Decrypt with (key1).

For many applications, you can use the same key for both key1 and key3 without creating a significant vulnerability.

Triple DES appears to be roughly as secure as single DES would be if it had a 112-bit key. How secure is this really? Suppose you had an integrated circuit which could perform one million Triple DES encryptions per second, and you built a massive computer containing one million of these chips to forcibly try all Triple DES keys. This computer, capable of testing 10 encryptions per second, would require: 

= 5.19 x 10 encryption operations 5.19 x 10 encryption operations / 10 operations/sec = 5.19 x 10 sec = 1.65 x 10 years.

This is more than 16,453 times older than the currently estimated age of the universe (approximately 10 years).

Apparently, barring new discoveries uncovering fundamental flaws or weaknesses with the DES algorithm, or new breakthroughs in the field of cryptanalysis, Triple DES is the most secure private key encryption algorithm that humanity will ever need (although niche opportunities may exist for faster algorithms).

RSA and Public Key Cryptography

RSA is the most widely known algorithm for performing public key cryptography. The algorithm is named after its inventors, Ronald Rivest, Adi Shamir, and Leonard Adleman, who made their discovery in the spring of 1977.

Unlike DES, which uses a single key, RSA uses two cryptographic keys: a public key and a secret key. The public key is used to encrypt a message and the secret key is used to decrypt it. (The system can also be run in reverse, using the secret key to encrypt data that can be decrypted with the public key.)

The RSA algorithm is covered by U.S. Patent 4,405,829 ("Cryptographic Communications System and Method"), which was filed for on December 14, 1977; issued on September 20, 1983; and expires on September 20. Because a description of the algorithm was published before the patent application was filed, RSA can be used without royalty everywhere in the world except the United States (international patent laws have different coverage of prior disclosure and patent applicability).[18] Not surprisingly, RSA is significantly more popular in Europe and Japan than in the United States, although its popularity in the U.S. is increasing.

[18] Ongoing controversy exists over whether this, or any other patent granted on what amounts to a series of mathematical transformations, can properly be patented. Some difference of opinion also exists about the scope of the patent protection. We anticipate that the courts will need a lot of time to sort out these issues.

How RSA works

The strength of RSA is based on the difficulty of factoring a very large number. The following brief treatment does not fully explain the mathematical subtleties of the algorithm. If you are interested in more detail, you can consult the original paper[19] or a text such as those listed in Appendix D.

[19] Rivest, R., Shamir, A., Adleman, L., "A Method for Obtaining Digital Signatures and Public Key Cryptosystems," Communications of the ACM, Volume 21, Number 2, February 1978.

RSA is based on well-known, number-theoretic properties of modular arithmetic and integers. One property makes use of the Euler Totient Function, [phi](n). The Totient function of a number is defined as the count of integers less than that number that are relatively prime to that number. (Two numbers are relatively prime if they have no common factors; for example, 9 and 8 are relatively prime.) The Totient function for a prime number is one less than the prime number itself: every positive integer less than the number is relatively prime to it.

The property used by RSA was discovered by Euler and is this: any integer i relatively prime to n raised to the power of [phi](n) and taken mod n is equal to 1. That is:

equation goes here

Suppose e and d are random integers that are inverses modulo [phi](n), that is:

equation goes here

A related property used in RSA was also discovered by Euler. His theorem says that if M is any number relatively prime to n, then:

and equation goes here

Cryptographically speaking, if M is part of a message, we have a simple means for encoding it with one function:

equation goes here

and decoding it with another function:

equation goes here

So how do we get appropriate values for n, e, and d? First, two large prime numbers p and q, of approximately the same size, are chosen, using some appropriate method. These numbers should be large - on the order of several hundred digits - and they should be kept secret.

Next, the Euler Totient function [phi](pq) is calculated. In the case of n being the product of two primes, [phi]( p q ) = ( p - 1 ) ( q - 1 ) = [phi](n).

Next, we pick a value e that is relatively prime to [phi](n). A good choice would be to pick something in the interval max ( p + 1, q + 1 ) < e <; [phi](n). Then we calculate a corresponding d, such that e d mod [phi](n) 1. That is, we find the modular inverse of e mod [phi](n). If d should happen to be too small (i.e., less than about log2(n)), we pick another e and d.

Now we have our keys. To encrypt a message m, we split m into fixed-size integers M less than n. Then we find the value (Me) mod n = s for each portion of the message. This calculation can be done quickly with hardware, or with software using special algorithms. These values are concatenated to form the encrypted message. To decrypt the message, it is split into the blocks, and each block is decrypted as (sd) mod n =M.

An RSA example

For this example, assume we pick two prime numbers p and q: 

p = 251 q = 269

The number n is therefore: 

n = 251 * 269 = 67519

The Euler Totient function for this value is: 

[phi](n) = (251-1) (269-1) = 67000

Let's arbitrarily pick e as 50253. d is then: 

d = e-1 mod 67000 = 27917

because: 

* 27917 = 1402913001 = 20939 * 67000 + 1 = 1 ( mod 67000 )

Using n = 67519 allows us to encode any message M that is between 0 and 67518. We can therefore use this system to encode a text message two characters at a time. (Two characters have 16 bits, or 65536 possibilities.)

Using e as our key, let's encode the message "RSA works!" The sequence of ASCII characters encoding "RSA works!" is shown in the following table

RSA Encoding Example
ASCII Decimal Value Encoded Value
"RS"
"A"
"wo"
"rk"
"s!"

As you can see, the encoded values do not resemble the original message.

To decrypt, we raise each of these numbers to the power of d and take the remainder mod n. After translating to ASCII, we get back the original message.

When RSA is used for practical applications, it is used with numbers that are hundreds of digits long. Because doing math with hundred-digit-long strings is time consuming, modern public key applications are designed to minimize the number of RSA calculations that need to be performed. Instead of using RSA to encrypt the entire message, RSA is used to encrypt a session key, which itself is used to encrypt the message using a high-speed, private key algorithm such as DES or IDEA.

Strength of RSA

The numbers n and either e or d can be disclosed without seriously compromising the strength of an RSA cipher. For an attacker to be able to break the encryption, he or she would have to find [phi](n), which, to the best of anyone's knowledge, requires factoring n.

Factoring large numbers is very difficult - no known method exists to do it efficiently. The time required to factor a number can be several hundred years or several billion years with the fastest computers, depending on how large the number n is. If n is large enough, it is, for all intents and purposes, unfactorable. The RSA encryption system is therefore quite strong, provided that appropriate values of n, e, and d are chosen, and that they are kept secret.

To see how difficult factoring a large number is, let's do a little rough calculation of how long factoring a 200 decimal-digit number would take; this number is more than 70 digits longer than the largest number ever factored, as of the time this tutorial went to press.

All 200-digit values can be represented in at most 665 binary bits.

  1. has digits.equation goes here

(In general, to factor a 665-bit number using one of the fastest-known factoring algorithms would require approximately 1.2 x 10 operations.)

Let's assume you have a machine that will do 10 billion (10) operations per second. (Somewhat faster than today's fastest parallel computers.) To perform 1.2 x 10 operations would require 1.2 x 10 seconds, or 380,267 years worth of computer time. If you feel uneasy about having your number factored in 380,267 years, simply double the size of your prime number: a 400-digit number would require a mere 8.6 x 10 years to factor. This is probably long enough; according to Stephen Hawking's A Brief History of Time, the universe itself is only about 2 x 10 years old.

To give you another perspective on the size of these numbers, assume that you (somehow) could precalculate the factors of all 200 decimal digit numbers. Simply to store the unfactored numbers themselves would require approximately (9 x 10) x 665 bits of storage (not including any overhead or indexing). Assume that you can store these on special media that hold 100GB (100 x 1024 or approximately 1.1 x 10) of storage. You would need about 6.12 x 10 of these disks.

Now assume that each of those disks is only one millionth A Brief History of Time, the universe itself is only about 2 x 1010 of a gram in weight (1 pound is 453.59 grams). The weight of all your storage would come to over 6.75 x 10 tons of disk. The planet Earth weighs only 6.588 x 10 tons. The Chandrasekhar limit, the amount of mass at which a star will collapse into a black hole, is about 1.5 times the mass of our Sun, or approximately 3.29 x 10 tons. Thus, your storage, left to itself, would collapse into a black hole from which your factoring could not escape! We are not sure how much mass is in our local galaxy, but we suspect it might be less than the amount you'd need for this project.

Again, it looks fairly certain that without a major breakthrough in number theory, the RSA mechanism (and similar methods) are almost assuredly safe from brute-force attacks, provided that you are careful in selecting appropriately prime numbers to create your key.

Factor This!

Not a year goes by without someone claiming to have made a revolutionary breakthrough in the field of factoring - some new discovery which "breaks" RSA and leaves any program based upon it vulnerable to decoding.

To help weed out the frauds from the real findings, RSA Data Security has created a challenge list of numbers. Each number on the list is the product of two large prime numbers. When the folks at RSA are contacted by somebody who claims a factoring breakthrough (and usually promises to keep the breakthrough a secret in exchange for some cash), they give the person a copy of the RSA challenge numbers.

The first RSA challenge number was published in the August 1977 issue of Scientific American. The number was 129 digits long, and $100 was offered for finding its factors. The RSA-129 number was solved in the fall of 1994 by an international team of more than 600 volunteers.

A month later, a researcher at the MIT AI Laboratory contacted one of the authors of this chapter, claiming a new factoring breakthrough. But there was a catch: to prove that he had solved the factoring problem, the researcher had factored that same RSA-129 number.

Nice try. That one has already been solved. If you are interested in the fame and fortune that comes from finding new factoring functions, try factoring this: 

RSA-140 = 2129024631825875754749788201627151749780670396327721627823338321538194 9984056495911366573853021918316783107387995317230889569230873441936471

If you factor this number, you'll get more than fame: you'll get cash. RSA Data Security keeps a "jackpot" for factoring winners. The pot grows by $1750 every quarter. The first quarter of 1995, it was approximately $15,000.

You can get a complete list of all the RSA challenge numbers by sending an electronic mail message to challenge-rsa-list@rsa.com.

An Unbreakable Encryption Algorithm

One type of encryption system is truly unbreakable: the so-called one-time pad mechanism. A one-time pad is illustrated in Figure 6.4.

The one-time pad often makes use of the mathematical function known as exclusive OR (XOR,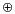(+)). If you XOR a number with any value V, then you get a second, encrypted number. XOR the encrypted number with value V a second time, and you'll get your starting number back. That is:

message = M

ciphertext = M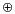(+)V

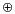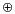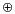plaintext = ciphertext(+)V = ((M(+)V)(+)V)

A system based on one-time pads is mathematically unbreakable (provided that the key itself is truly random) because you can't do a key search: if you try every possible key, you will get every possible message of the same length back. How do you tell which one is correct?

Unfortunately, there is a catch: to use this system, you need to have a stream of values - a key, if you will - that is at least as long as the message you wish to encrypt. Each character of your message is XOR'ed, bit by bit, with each successive character of the stream.

Figure 6.4: A one-time pad

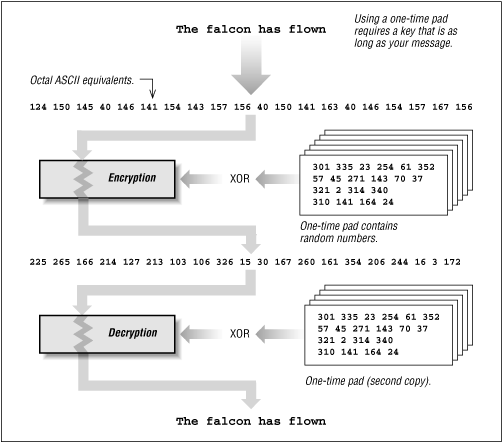
Figure 6.4

One-time pads have two important vulnerabilities:

  1. The stream of random values must be truly random. If there is any regularity or order, that order can be measured and exploited to decode the message.
  2. The stream must never be repeated. If it is, a sophisticated cryptanalyst can find the repeats and use them to decode all messages that have been encoded with the no-longer one-time pad.

Most one-time pads are generated with machines based on nuclear radioactive decay, a process that is believed to be unpredictable, if not truly random. Almost every "random number generator" you will find on any standard computer system will not generate truly random numbers: the sequence will eventually repeat.

To see how this encryption mechanism works in practice, imagine the following one-time pad:

With this sequence, the message: 

UNIX is secure.

Might encrypt as follows: 

:\:\:s*:3:\rEs[drNERwe.

Which is really a printed representation of the following string of values:

To use a one-time pad system, you need two copies of the pad: one to encrypt the message, and the other to decrypt the message. Each copy must be destroyed after use; after all, if an attacker should ever obtain a copy of the pad, then any messages sent with it would be compromised.

One of the main uses of one-time pads has been for sensitive diplomatic communications that are subject to heavy monitoring and intensive code breaking attempts - such as the communication lines between the U.S. Embassy in Moscow and the State Department in Washington, D.C. However, the general use of one-time pads is limited because generating the sequence of random bits is difficult, and distributing it securely to both the sender and the recipient of the message is expensive.

Because of the problems associated with one-time pads, other kinds of algorithms are normally employed for computer encryption. These tend to be compact, mathematically based functions. The mathematical functions are frequently used to generate a pseudorandom sequence of numbers that are XOR'ed with the original message - which is similar to the way the one-time pad works. (For example, Jim Bidzos, president of RSA Data Security, likes to call its RC4 stream cipher a "one-time pad generator," although the cipher is clearly not such a thing.) The difference between the two techniques is that, with mathematical functions, you can always - in principle, at least - translate any message encrypted with these methods back into the original message without knowing the key.

Proprietary Encryption Systems

The RC4 algorithm mentioned in the previous section is an example of a so-called proprietary encryption algorithm: an encryption algorithm developed by an individual or company which is not made publicly available.

There are many proprietary algorithms in use today. Usually, the algorithms are private key algorithms that are used in place of algorithms such as DES or IDEA.[20] Although some proprietary systems are relatively secure, the vast majority are not. To make matters worse, you can rarely tell which are safe and which are not - especially if the company selling the encryption program refuses to publish the details of the algorithm.

[20] While creating a public key encryption system is difficult, creating a private key system is comparatively easy. Making a private key system that is secure, on the other hand, is a considerably more difficult endeavor.

A standard tenet in data encryption is that the security of the system should depend completely on the security of the encryption key. When choosing an encryption system, rely on formal mathematical proofs of security, rather than on secret proprietary systems. If the vendor of an encryption algorithm or technology will not disclose the algorithm and show how it has been analyzed to show its strength, you are probably better off avoiding it.

The RC4 algorithm is no exception to this tenet. In 1994, an unknown person or persons published source code that claimed to be RC4 on the Internet. By early 1996, a number of groups around the world had started to find minor flaws in the algorithm, most of them having to do with weak keys. Although RC4 appears to be secure for most applications at this time, the clock may be ticking.